Contents

The statistics of extremes is about modelling scenarios that we haven’t experienced (or very rarely experience), based on scenarios that we have. This, of course, has a greater uncertainty than non-extreme statistical modelling and methods. Extreme value modelling can be used to model the frequency of natural disasters, such as hurricanes, floods, earthquakes and volcanoes. It can also be useful for modelling financial crashes, medical outbreaks, terrorist attacks and can then be used to avoid, mitigate or adapt to them in the future. With extreme value methods we can model the answers to questions such as; what is the probability that a magnitude 9 earthquake will occur in San Francisco next year? Or what is the magnitude of a flood that will be exceeded only once every 100 years on average? Or how big are the waves during the 50 year storm on Bells Beach?* If we know the 100-year river flow and associated water level, we can determine where the flood would go and how many properties would be flooded. Similarly, if a location floods and we estimate the probability of equalling or exceeding the river flow that caused it, we can determine how often it will flood in the future. This section outlines, in simple terms, without too much mathematics, the general methods of extreme value analysis (with an emphasis on flood hydrology). 

*See ‘Point Break’ - directed by Katherine Bigelow, starring Patrick Swayze and Keanu Reeves. It should be noted that the movie seems to suggest we can know when a 50 year storm will occur because it’s regular. This is not so, we can only estimate the magnitude of a 50 year event, or the frequency with which a given magnitude will be exceeded. A storm of the 50 year magnitude could be exceeded three times in one year or not at all over 100 years, but over an infinite period it would average out to once every 50 years.

Firstly, for estimating extremes values, if we had enough data, we could do it empirically. If we wanted to estimate the 100-year flow from observed data at a river gauge and we had a million years worth of daily peak flows, we can estimate the flow with confidence. To see how, lets first define the probability of an event of interest occurring as: the number of events of interest divided by the total number of events. This can also be considered as the proportion of events of interest over all events. The 100-year flow is the flow that is exceeded, on average, once every 100 years. Therefore the proportion (1/100 = 0.01) of annual maximum peaks will be above the 100-year flow. Now, with our one million years of daily peak flow data, we can extract the annual maximum values for each year and order them from highest to lowest. With our ordered flow we can find the appropriate rank of the 100-year flow as 0.01 x 1,000,000 = 10,000. The flow at the 10,000th rank is our 100-year flow. However, we don’t have a million years of data and usually don’t have 100 years either. Instead we need to “model” distributions of data such as our annual maximum peaks. This modelling is the essence of extreme value theory.

Before we can understand the modelling of extreme values, we first need to understand the concept of probability distributions. You may also see them referred to as statistical distributions, frequency distributions, statistical models or simply distributions.

When enough data is collected and plotted on a frequency graph (histogram), a shape becomes clear. The more data that is collected the more defined this shape becomes. With more data we can decrease the width of the intervals of our bars and increase the number of them. We can join the tops of the bars with a curve and with enough data the intervals could be so small that individually they would not be visible and they would form a homogenous area under the curve.

For example, below (figure 1) are two graphs showing the heights of adult males. They have the same underlying distribution (the normal/Gaussian distribution). The first graph has a sample of 40 and the second has a sample of 10,000. The shape is more defined for the sample of 10,000. The sample of 40 is taken from the larger sample of 10,000. They are from the same parent population.

These shapes have known mathematical properties and parameters that define them. For example, the normal distribution can be defined by the mean value (average) and the standard deviation (a measure of the variance of the data). With an estimation of these two parameters from the data, we can infer/model an infinite sample size.

There are two important assumptions to consider. Firstly, each data point in the sample is assumed to be from the same underlying distribution and independent of any other. That is, each data point has no influence on any other. Secondly it is assumed that there is no trend in the data. For example applying the extreme value methods, outlined here, to rising sea levels or river flows that are increasing over time, would provide estimates that are too low. There are ways to take trend into account, such as detrending the data or adjusting individual parameters, but they are not covered here (they’re used in the London flood mapping example).

2.1 CDF and PDF

Distributions can be considered in terms of the probability density function (PDF) or the cumulative distribution function (CDF). An example of both, for the heights of adults, can be seen below in fig 2. The distribution is assumed normal with a mean of 176cm and standard deviation of 7cm. The PDF provides a probability of given values occurring*, whereas the CDF is the cumulative probability of the PDF; or the area under the PDF curve up to a given value. For example, looking at the PDF of heights in fig 2 on the right, we can see that there is 0.0569 probability of randomly selecting a male with a height of 176cm* (red line). The CDF provides the sum of probabilities up to the height of 176cm (it’s the proportion of the distribution below that point). As 176cm is the central value, the CDF is 0.5 because the sum of all the probabilities is 1 and the central value is half way (illustrated in fig 2, on the left, in red). Another example would be the height of 184cm. For 184cm the PDF is 0.02966 and the CDF is 0.87 (green lines). In flood estimation we’re interested in the exceedance probability which is the inverse of the CDF i.e. for the last example; 1 minus 0.87 (the proportion of the distribution above that point). This provides 0.13, so we can say that there is a 0.13 probability of randomly selecting a male with a height greater than 184cm. That would be a 13% chance, or in terms of frequency it would be 1 in 8 males (because 1/8 = 0.13 and 1/0.13 = 8). Which means, on average, over many random selections, we would select a male who is taller than 184cm once in every 8 selections. The CDF is usually denoted f(x), which should be read as f of x or function of x, whereas the PDF is usually denoted as p(x) which should be read as p of x or probability of x. Where x is the variable under consideration, on this occasion, the height of adult males. 

One last point to note about distributions; the above is in reference to continuous distributions. Continuous distributions are made up of values that can be any value on the number line, with any number of decimal points. Discrete distributions are made up of finite values with a minimum distance between two values, usually integers. In the case of discrete distributions the probability density function is referred to as the probability mass function (PMF). For example, river flow is continuous whereas the number of flood events in a given time period is discrete. One simplified comparison is: discrete data is countable whereas continuous data is not.

*in fact, the probability of any one value occurring is infinitely small (or zero) because it’s a continuous distribution and there are an infinite number of values between any two values. In essence the calculation is the integration of area under the PDF curve, between two intervals. In the example here, the interval on the real number line that makes up the value 176 (approximately 175.5 to 176.5). The result of the integration is the density (hence the term density function) and the total density of the curve (or area under the curve) equals one.

2.2 Non-Gaussian distributions

Not all distributions are normal of course, which means different models and parameters are needed to describe them. Some have a skew which means that the distribution shape is not symmetrical. In such situations a shape parameter is needed to infer larger samples. In a normal distribution, the mean is the same as the median (middle value). A distribution that has a skew would have different values for mean and median.

Many hydrological distributions are positively skewed. Below is an example of annual maximum rainfall for a daily duration. There is a sample size of 40 and a sample size of 10,000. As the sample size increases, a distribution shape starts to become clear and this is the generalised extreme value distribution (GEV). This data is simulated; I couldn’t find a rain gauge that was 10,000 years old.

For flood frequency analysis we generally want to estimate one of two things; the probability of exceeding an observed flow event or a design flow (the flow associated with a given exceedance probability). In both cases the probability in which we are interested is the exceedance probability = 1 - f(x). The design flow is that which we estimate as being exceeded, on average, once in a given time period (QT) *. The latter is the reciprocal of the former; QT = 1/ 1-f(x) i.e. return period = 1 / probability of exceedance. Therefore the design flow for the 100-year return period is the flow that will be exceeded, on average, once every 100 years. More generally the design flow is referred to as the return level (the level associated with the return period). In flood hydrology you may also see it called the flood or flow quantile.

To summarise:

Return Period (T): The return period (T) of a flow is a measure of its rarity, defined as the average interval between occurrences of flows that exceed it. The longer the return period the rarer the flow.

Exceedance Probability: The probability that a given flow will be exceeded in a given time period. The time period is usually a year, which makes it an annual exceedance probability (AEP). The AEP is often expressed as a percentage which is the probability multiplied by 100.

3.1 Extreme Value Methods

When assessing extreme values, we are unfortunately wasteful in that we don’t make use of the majority of our data. We use only the larger values in the sample. There are two common approaches; block maxima and threshold exceedance; both make up distributions and can be used to provide us with a T year flow.

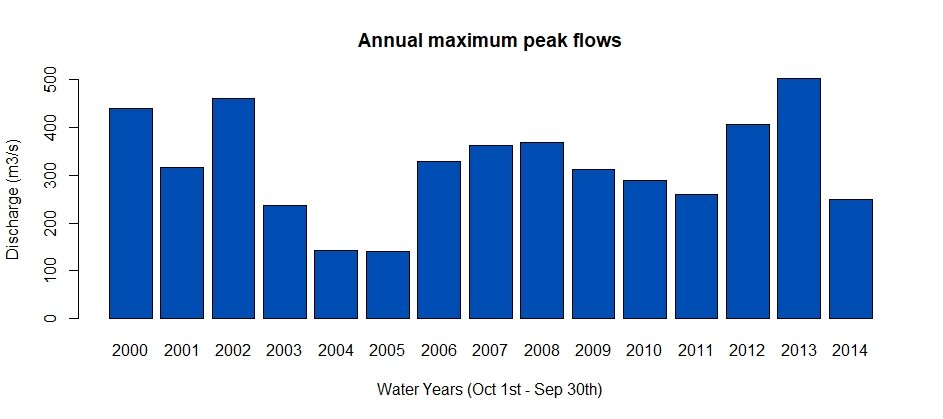
The block maxima approach takes the largest data values for given time periods, usually a year, which leaves us with the AMAX (annual maximums). This AMAX is then assumed to follow a specific distribution so that the return periods can be derived. This provides TAM, which is the average interval between years containing one or more flows exceeding a given value (Q.TAM).

Threshold Exceedance is not time dependent and instead uses a cumulative probability level, below which the data is discarded and above which it is used in the analysis. The threshold is chosen in a balance between bias and variance. If the threshold is lower there is more data, but if it’s too low a bias can result. If it’s too high, there is less data and therefore more uncertainty. As with the block maxima approach, the data are assumed to be independent and therefore care is needed when extracting the peaks. This method is also known as peaks over threshold (POT) and provides TPOT which is the average interval between floods exceeding a given value Q.TPOT.

The approximate relationship between TAM and TPOT is:

The POT method allows multiple floods in one year and therefore TPOT is always shorter than TAM but the difference is insignificant for return periods >20 years. It should be noted that both approaches assume the peaks used are independent of each other. If the flow regime of the river has a slow response, it may be that there are no more than one independent peak per year. In which case the block maxima approach may be preferable. This would be the case for very large and/or permeable catchments.

Which to choose; block maxima or peaks over threshold?

The benefit of the POT method is the use of more data which reduces the uncertainty in estimates. It would, therefore, be preferable for short records at the least. However, uncertainty is increased by the choice of a threshold and by the method to extract the peaks whilst ensuring they are independent. These extraction methods for POT are usually based on de-clustering algorithms and assume that peaks are independent if separated by a given time frame or number of non-extreme peaks. Another approach is to assume that peaks are independent if the time series has returned to a mean value (or some other low threshold) between them. Either way, choices are made for the threshold and the extraction method, both of which add to the variance of results. Arguably, POT is more subjective. However, a POT series with, on average, one peak per year usually has slightly less variance than an AMAX series of the same length. This is because the POT series is forced to be above a certain level whereas the AMAX sample can include values below the level (expanding the possible variance in comparison). The POT approach also ensures that we capture all the flood events (there may be more than one a year) whereas the AMAX only uses the largest of each year, some of which may not be considered extreme. The choice, as you can see, is not straight forward.

3.2 Distributions for Extreme Values analysis

For the block maxima approach the extreme value theorem suggests; as the sample of block maxima increases, the distribution shape will converge to one of three distributions; the Gumbel, Frechet and Weibull. Also known as EV1, EV2 and EV3 respectively (where EV stands for extreme value). These can be generalised by the Generalised Extreme Value Distribution (GEV), which was recommend in the flood studies report (1975) for extreme flow analysis. In the flood estimation handbook(1999) the recommendation was changed to the generalised logistic distribution (GLO) as it was empirically seen to better fit a wider range of AMAX flows in the UK. It may seem strange that, given the extreme value theory, a different distribution is used. This is because the distributions have assumptions that are only approximately met by the flow data and how it is used.

When a threshold exceedance approach is taken the EV distributions aren’t suitable because the distribution tail is more specifically modelled. In this case the generalised Pareto (GP) distribution is used instead. The GP distribution specifically models the tails of distributions and can be applied to the tails of data with different underlying shapes. An example would be for modelling rainfall. The distribution shape changes depending on the rainfall duration being modelled. Broadly speaking daily values would follow an exponential distribution, monthly a gamma distribution and yearly a normal distribution. For extreme value analysis the tails of distributions from different durations (hourly rainfall, daily, etc) can be specifically modelled using the GP distribution and the AMAX of them with a GEV.

3.3 Parameter Estimation

Before a distribution can be used to provide estimates based on the data, the parameters of the distribution have to be estimated. The parameters are quantitative descriptions of the parent population from which the data is sampled. We estimate these based on the sample we have, by calculating the statistics; where statistics are estimates of parameters. Commonly known statistics are the measures of central tendency such as mean, median and mode and also measures of data spread such as variance and standard deviation. Distributions used in extreme value analysis have two to three parameters known as; location, scale and shape (which are akin to mean, standard deviation and skew, respectively).

Three common approaches for estimating parameters are; the method of moments, maximum likelihood estimation and L-Moments.

Method of Moments: is the simplest in the sense that there are equations, one for each parameter, that estimate the parameter directly from the sample. The first four moments are the statistics; mean, variance, skewness (a measure of symmetry) and kurtosis (how peaky is the distribution). They are all, in some form, measures of variation from the mean.

The maximum likelihood estimation (MLE) approach is more flexible in that it can be used when analytical solutions such as the method of moments aren’t defined. The MLE method is a little more complicated and benefits from a mathematical optimiser. But generally speaking, the method fits the distribution to the data using a guess at the parameters and calculates the likelihood of the parameters, given the observed data. The values for these parameters are changed iteratively until the likelihood is maximised. The parameters providing the maximum likelihood are then taken as the best estimate.

L-Moments: One problem with estimating parameters, especially with skewed data, is the impact of outliers on the results*. To reduce this problem, the order of the observations in the sample can be used. The first four L-moments are; L-Location, L-scale, L-skewness and L-kurtosis. The 2nd to 3rd L-moments are similar to conventional moments but rather than being based on observations and their variation from the mean, the observations are weighted by a probability. A probability based on the rank of the observation. This has been seen to work better than MLE for small samples sizes (Hosking & Wallis, 1997).

*An analogy here would be the press quoting remarkably high figures for the price of an average wedding. They are usually quoting the mean which is heavily skewed by >million pound weddings. This average is therefore not indicative of the “usual” amount paid for a wedding. i.e. if one were to pick a wedding at random, what is the likely cost? The median would be a more appropriate measure in this sense. However, it’s not used because it doesn’t create a juicy story. Having said that; the first L-moment is the arithmetic mean.

The annual maximum flow data at a gauge is a small sample of what can be considered an infinite population. For this reason the sample doesn’t perfectly represent the population and we have what is referred to as sampling error. The parameters derived from the sample as statistics, are an estimate of the population parameters and there is uncertainty within that estimate. Therefore there is uncertainty within any inferred value we estimate such as the 100-year flow. This uncertainty is from the sampling error and the assumptions of the model we use for our estimates. To quantify our uncertainty we can calculate confidence intervals around our central estimate. Confidence intervals provide a range within which we are confident that the true value resides*. The more confident we want to be, the wider the intervals and vice versa. There is a trade-off between having greater confidence with intervals that are too wide and having less confidence with intervals that are nice and thin. It is important to note that the central estimate is still the best estimate and is considered more likely to be the true value than the upper or lower interval values. 

*The percentage attributed to our confidence intervals (such as 95%) indicates that over a large number of samples of the same size, 95% of all the confidence intervals we calculated, using the same method, would contain the true value. Clearly, if we had all those samples we’d use them in the estimate. However, it’s important conceptually. It’s different from having 95% chance of containing the true value within our confidence intervals.   

4.1 Deriving confidence intervals

There are analytical ways to provide confidence for many distributions. i.e. equations can be used directly. Not all distributions have such analytical expressions. A common approach to deriving confidence intervals for extreme value analysis is bootstrapping, which is a versatile resampling technique. The idea is that we have a sample, of which we are relatively certain, because it was recorded. We can be confident that those AMAX flows (or similar flows) could be recorded again or could have been recorded in any other order or combination, given different but plausible scenarios. Therefore we can re-do the estimate of our extreme flow many times (let’s say 199), with the same data in many different combinations, but with the same sample size. Our 199 samples are made up by randomly selecting from the original sample with replacement after each selection.  Another way of looking at it is; we copy our sample 199 times, then jumble all of these copies up together randomly, then split it back up into 199 samples, the same size as the original sample (balanced resampling). We then re-estimate on each new sample. After we have 199 new estimates of our extreme flow, we have a distribution of estimates and this distribution is approximately normal (due to the central limit theorem). The upper 97.5% estimate is then our upper 95% interval and the lower 2.5% estimate is our lower 95% interval. As we have 199 estimates we can list them in order, the 5th lowest and the 5th highest are the 95% intervals and the 32nd lowest and the 32nd highest would be the 68% intervals. 68% and 95% intervals cover approximately one and two standard deviations from the mean of a normal distribution respectively. If the sampling distribution (distribution of estimates) is assumed to be normal (not always an appropriate assumption), we can also use the associated mean and standard deviation (i.e. of the bootstrapped estimates) to quantify our uncertainty. The mean of the estimates plus and minus one standard deviation of all the estimates provides 68% intervals, and the mean plus and minus 1.96 times the standard deviation provides 95% intervals. For example, the annual maximum flow sample at Kingston on the Thames is over 135 years long. Figure 6 below provides a histogram of 10,000 bootstrapped 100-year peak flow estimates for the Kingston AMAX sample (using the generalised logistic distribution). The mean of the distribution of estimates (the sampling distribution) is 700m3/s and the standard deviation is 55m3/s. The 95% confidence interval are therefore: 700 - 55*1.96 = 592 and 700 + 55*1.96 = 808. Similarly 68% intervals would be 645 & 755, which are shown in red in figure 6 (68% of the sampling distribution is between the intervals). Similarly the approach can be done in a parametric way (a parametric bootsrap) where the numerous samples are simulated by the assumed distribution instead of sampled with replacement from the observations.

A fundamental difficulty with extreme value analysis is the lack of data in the extremes. Extreme events are, by definition, rare. Often we have no gauged data at all. One method to overcome such a difficulty is regional frequency analysis (with this nomenclature regions aren’t necessarily geographic). This involves using data from groups of similar sites (regions) to supplement the data (or lack of) at the site of interest. The assumption is that sites of similar characteristics will have the same underlying distribution* and only differ due to an index flood; a site specific scaling factor. With this assumption we can estimate a flood frequency for all the sites in the region (pooling group is the term used in the UKs flood estimation handbook FEH) and take a weighted average as our best estimate. In the case of the recommended flood frequency procedures in the UK, the index flood is the median annual maximum flow (QMED).

For example; we could estimate the 100-year return period flow for 15 sites similar in catchment characteristics to the site of interest. We could then divide each of these by their QMED, providing a growth factor for the 100-year flow**. To get a pooled estimate, an average of those growth factors could be used. If we then estimate QMED at the site of interest and multiply it by the pooled (averaged) growth factor, we have our estimate of the 100-year flow. With no data at the site of interest the QMED can be derived with a regression equation, trained on sites with gauged records, linking observed QMED with catchment characteristics. There are a few options for forming regions such as the region of influence approach (used in the FEH), geographical or derived through cluster analysis. Similarly there are different ways for estimating the index flood, such as regression or rainfall runoff modelling.

*The “true” standardised parameters are the same and any variation in them and the associated growth curve is assumed to be due to sampling error (the variance between statistics of a sample and statistics of the population).

**This is merely illustrative, the growth factor is generally calculated without this step, using the parameters of the assumed distribution. For example In the FEH procedures, a weighted average of the standardised distribution parameters (L-moment Ratios; L-CV and L-SKEW) of each site, is used to estimate the growth factor.

Often in hydrological analysis there are multidimensional problems. For example we may wish to determine the joint probability of flows at more than one location. Or determine likely flows on river B given that river A reaches a particular return level. If there is no dependence between the flows at the locations, they are said to be independent and the problem becomes trivial. If flows are independent it means they’re not affected by a mutual phenomenon and don’t impact each other. In which case they’re not correlated (or if they are it’s by chance). With no dependence we simply multiply the return periods, or probabilities, to derive the joint return period or probability. If the flows are correlated a dependence structure needs to be defined. To simulate extreme flows or rainfall, pseudo-random numbers can be developed and the distribution of choice, such as those discussed above, can be used to calculate associated flows or rain*. For the bivariate case (two rivers or rainfall points for example) it’s necessary to simulate two variables whilst maintaining the way they vary together (their covariance). With hydrological variables this covariance changes as a function of magnitude - in the extremes the covariance is different from the covariance more frequently experienced.

6.1 Copulas:

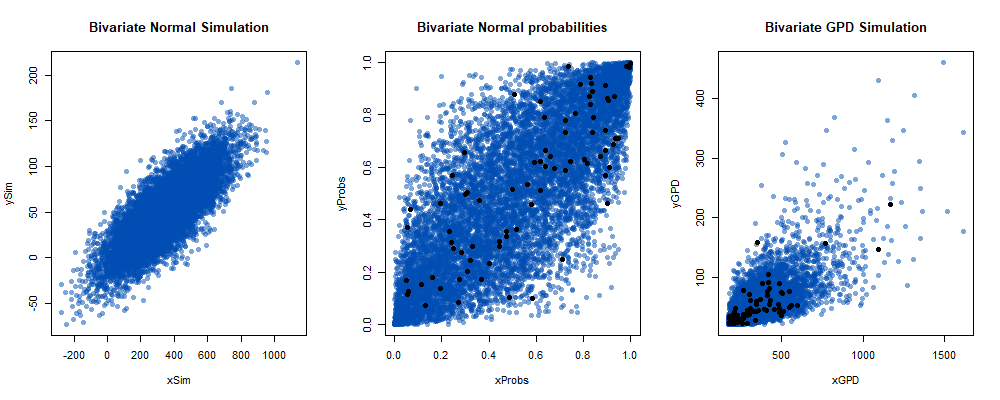
Many distributions, such as those we use to model flood extremes, don’t have a defined multivariate probability function. Some distributions, such as the normal distribution, do have a multivariate form. This can be used to form a copula. A copula is a model of the covariant cumulative probabilities between two or more variables. For example, figure 7 shows concurrent flows on two rivers (the Eden and the Caldew at Carlisle). The blue dots were simulated using a Gaussian copula (bivariate normal distribution) - 10,000 of them. The temporally independent & concurrent values above the chosen threshold were modelled/simulated as if they were normally distributed and had a normally distributed covariance structure. i.e. the POT data was extracted from the Eden along with the the concurrent peak at Caldew (taking the maximum at Caldew over a one day event window - one day duration either side of the peak at Eden). They were then modelled with their means, standard deviations, and correlation coefficient using a bivariate normal distribution. The associated normal distribution probabilities were calculated for each simulated value for both variables. Then the generalised Pareto distribution for both variables was used to convert those probabilities into Generalised Pareto distributed (GPD) flows. And, as if by magic, bivariate GPD variables have been simulated (the result of each step is illustrated in figure 8). This approach can be extended to any number of variables using the multivariate normal distribution. Many different copulas are available and any distribution can be used to transform the simulated covariant probabilities to form the final simulated variables . For independent peaks above a high threshold, the GPD is usually assumed.

6.2 Heffernan and Tawn model

However, some argue that such dependence structures are too rigid and not flexible enough to model many naturally occurring multivariate extreme covariance structures. One approach that is now commonly used in the UK is a model known as the Heffernan and Tawn model 2004 (HT04). It is a conditional extremes model which fits a non-linear function between a site of choice (the conditioning variable) and multiple other dependent sites (marginal variables). The variables are first transformed to a standardised Gumbel distribution (or more commonly, now, Laplace). The dependence structure is based on concurrent observations at all the gauges and therefore there are concurrent residuals for each (residuals in this case are deviations from a modelled result). Thousands of values are simulated for the conditioning variable using the standardised Gumbel distribution. The non-linear functions then provide estimated values for each marginal variable and the concurrent residuals are bootstrapped (see section 'deriving confidence intervals') and added to these randomly. This simulates values at all the gauges whilst maintaining their dependence. The Gumbel probabilities are then calculated for each variable which are then transformed using the GPD (as with the above Gaussian copula example), providing the required extremes. The joint exceedance of these can be used to determine the joint probability.

6.3 What to do with the simulated results?

On the river Eden at Sheepmount is a gauge measuring discharge through Carlisle (it’s to the west of Carlisle and the Eden flows in a NW direction). There is another gauge on the river Caldew at Cummersdale also measuring discharge flowing through Carlisle (the gauge is to the South and the Caldew flows north). We might want to map/model the consequence of the 50-year or 100-year event through Carlisle. What peak flow do we choose for each gauge for a combined 50-year event? If we chose the 50-year event on both, the combined event would have a far longer return period than 50 (be less likely than the 1/50 = 0.02 annual exceedance probability) because the two sites are not perfectly correlated. We wouldn’t choose a 7-year event (approximate square root of 50) on both because they’re not independent. Using such simulations as those outlined above, the likely magnitude of one variable as a function of the other can be determined. If the simulation in figure 7 is subset so that all Caldew values are extracted where the Eden is between 1000 & 1025 m3/s (the 50-year return level is approximately 1015m3/s), there is a distribution of possible values on the Caldew. The mean of which is 177m3/s, which, for the Caldew, has an 18-year return period (n.b. these are daily mean flow peaks, instantaneous peaks would be higher). Therefore, if we were modelling a 50-year event for Carlisle we might use a 50-year flow on the Eden and an 18-year on the Caldew. The procedure can then be reversed, sub-setting for when the Caldew has a 50-year flow (approximately 230m3/s). In this case I subset between 225 and 235m3/s and the associated mean Eden flow is 906m3/s which has a 27-year return period. For the 50-year event these are highlighted in figure 9 (left and right red dots). As this is a stochastic process these results will differ for each simulation and there is of course uncertainty in the mean estimate of y conditional on x (and vice versa). Bootstrapping the mean conditionals and taking 95% intervals suggests the Caldew conditional on the Eden being a 50-year return level has a mean return period with 95% intervals of 10-years to 34-years. Likewise Eden conditional on the Caldew being at the 50-year return level has a mean return period with 95% intervals of 17-years to 45-years. A central option might also be modelled. What is the central option? As we’ve simulated so many events we can use the ranking method. Rank each variable and then sum the ranks - then rank these to get “event ranks”. The event ranks can be used to derive event return periods (e.g. 1/[rank/ N+1]), where rank 1 is high) which should then be divided by the number of peaks per year used in the analysis (to convert to annual RP). Joint events with a return period close to 50 years can then be extracted. A central event based on this subset would be the median of x and y (the central red dot in figure 9). Figure 9 also shows the subset of events with a 0.02 joint annual exceedance probability (the 50-year joint event) highlighted in green. Another option for more than two variables is to subset the simulation around a chosen conditioning variable (at the return level of choice), then this and the mean of all the other variables can be used as the conditional extremes event.

*This is known as a Monte Carlo approach. For example; if the pseudo random number generated is 0.01 and we were simulating an AMAX distribution, then the flow simulated would be the 100-year return period flow. i.e. we use the assumed distribution to estimate the 100-year flow.

COLES, S., 2001. An Introduction to Statistical Modeling of Extreme Values. Springer, London.

FAULKNER, D. S., 1999. Rainfall frequency estimation. Volume 2 Flood Estimation Handbook, Institute of Hydrology, Wallingford, UK.

HEFFERNAN, J. E. AND TAWN, J. A., 2004. A conditional approach for multivariate extreme values (with discussion). Journal of the Royal Statistical Society: Series B (Statistical Methodology) 66(3): 497-546

HOSKING, J. R. M. AND WALLIS, J. R., 1997. Regional Flood Frequency Analysis: an approach based on L-moments. Cambridge University Press, New York.

ROBSON, A. AND REED, D., 1999. Statistical procedures for flood frequency estimation. Volume 3 Flood Estimation Handbook, Institute of Hydrology, Wallingford, UK.

SUTCLIFFE, J. V., 1975. Methods of flood estimation: A Guide to the Flood Studies Report. IH Report No. 49, Institute of Hydrology, Wallingford, UK.